The Auto-regression and Decoding Strategies

Auto-regressive language generation assumes that the element of the output sequence at time-step $t$ is determined by the input sequence and time-steps before $t$. $$ P\left(w_{1: T} \mid W_0\right)=\prod_{t=1}^T P\left(w_t \mid w_{1: t-1}, W_0\right), \text { with } w_{1: 0}=\emptyset $$
where $W_0$ is the input sequence; $W_t$ is the word at timestep $t$; T is determined by the position of a token. source
Language models, especially those like the GPT and LLaMa, are auto-regressive. This means that they generate sequences one item at a time, using the previously generated items as context for generating the next item. When the Language model is given a series of tokens, it tries to guess what comes next. It does this by creating a list of discrete probability distributions for each potential next token using softmax. The decoding strategy is applied to select the next token(s) from this distribution. Due to the sequential structure of language, tokens must not only be contextually appropriate but also organically flow to create cohesive sentences and paragraphs. Decoding strategies help in selecting tokens that adhere to the patterns and structures of the language. Also, decoding strategies help strike a balance between deterministic outputs and creative, diverse responses.
The true beauty of these strategies is best appreciated when they are built from the ground up, understanding each decision and line of code that goes into making them work.
In this blog, we aim to demystify these decoding strategies. And how do we plan to do that? By doing everything from scratch! We won’t be relying on pre-built libraries or ready-made functions
Decoding Strategies
Before diving into the theoretical and practical aspects of each of the decoding strategies, let’s write a Sampler base class that abstracts the common utilities and operations, ensuring that subsequent decoding strategies can be implemented in a more streamlined manner. Its core functionalities are encoding text into token IDs, decoding these IDs back into text, and obtaining the next token’s probability.
Additionally, the class offers the ability to visually represent scores of tokens through the plot_scores method, displaying a color-coded bar graph of top token probabilities, thus providing an intuitive overview of the model’s predictions.
import torch
import plotly.graph_objects as go
from transformers import AutoTokenizer, AutoModelForCausalLM
# torch.manual_seed(0)
class Sampler:
def __init__(self , model_name : str ='gpt2-medium') -> None:
self.device = 'cuda' if torch.cuda.is_available() else 'cpu'
self.tokenizer = AutoTokenizer.from_pretrained(model_name)
self.model = AutoModelForCausalLM.from_pretrained(model_name).to("cpu").to(self.device)
def encode(self, text):
return self.tokenizer.encode(text, return_tensors='pt').to(self.device)
def decode(self, ids):
return self.tokenizer.decode(ids)
def get_next_token_prob(self, input_ids: torch.Tensor):
with torch.no_grad():
logits = self.model(input_ids=input_ids).logits
logits = logits[0, -1, :]
return logits
def plot_scores(self, scores, title, samples):
top_indices = torch.argsort(scores, descending=True)[:samples]
tokens = [self.decode(idx) for idx in top_indices]
if self.device == "cpu":
top_probs = scores[top_indices].numpy()
else:
top_probs = scores[top_indices].cpu().numpy()
colors = ['#E95B68', '#C4C956', '#58BB7B', '#CAC1C5', '#87601F', '#F7311B',
'#C53D39', '#38658F', '#242ABC', '#9DA52F', '#329018', '#D415C5',
'#6DCE59', '#ADF212', '#9CF042']
colors = colors[0:len(top_indices)]
fig = go.Figure(data=[
go.Bar(x=tokens, y=top_probs, marker_color=colors, textposition='auto')
])
fig.update_layout(title=title)
fig.show()
Greedy Search Decoding:
Greedy search is the simplest decoding method. It takes the token with the highest conditional probability from the vocabulary V.
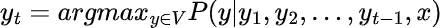
At each step, it selects the token with the highest probability and adds it to the sequence. It is continued until an end token is met or a maximum sequence length is reached.
import torch
class GreedySampler(Sampler):
def __call__(self, prompt, max_new_tokens=10):
predictions = []
result = prompt
# generate until max_len
for i in range(max_new_tokens):
input_ids = self.encode(result)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
# choose the token with the highest probability
id = torch.argmax(next_token_probs, dim=-1).item()
# convert to token and add new token to text
result += self.decode(id)
predictions.append(next_token_probs[id].item())
return result
We will be using the same SAMPLE_TEXT and an equal maximum sequence length when testing each decoding strategy. This we can easily assess the performance of each decoding strategy.
SAMPLE_TEXT = "Artificial Intelligence is the intelligence possessed by the”
greedy_sampler = GreedySampler()
result = greedy_sampler(prompt=SAMPLE_TEXT,max_new_tokens=16)
print(result)
Output:
Artificial Intelligence is the intelligence possessed by the machines that run the world. It is the intelligence that is capable of understanding and
Greedy search is advantageous due to its simplicity and computational efficiency. By tracking only the most probable sequence, it requires less memory and computational power. However, there are some major drawbacks to this approach:
- Myopia: Greedy algorithms focus solely on the best immediate option, overlooking potential long-term benefits. It’s like a hiker only choosing the nearest hilltop without aiming for the tallest mountain.
- Repetitiveness: These algorithms often produce generic and monotonous outputs. By always picking the most probable word, it tends to favor frequently used phrases, leading to predictable results.
- Error Magnification: Greedy search can’t rectify its mistakes. Once it makes a less-than-ideal choice, every subsequent decision is influenced.
Beam Search:
Beam search is an advanced decoding algorithm designed to optimize sequence generation.
Unlike the greedy search that might consider only the most probable word at each step, beam search simultaneously tracks multiple potential sequences, determined by a parameter known as the ‘beam width’.
At every stage, it expands each sequence by appending all possible subsequent words. From this pool of new sequences, the top ‘k’ sequences will be selected, where ‘k’ signifies the beam width. This ensures that the algorithm doesn’t just focus on immediate high-probability words, but also on the overall sequence probability. In essence, beam search aims to balance between finding the most probable sequence and computational efficiency by considering multiple sequences but not every possible one.
While the outcome of beam search decoding is notably more fluent, it may contain repeated sequences of the same words. To address this repetition, the concept of “n-gram penalty” can be used. This technique ensures that any given n-gram only appears once. If a n-gram sequence is generated to put in sequence and that n-gram is already present in the sequence, then its probability is set to zero.
Let’s take an example where we search through the graph to obtain a sequence length of 4, pruning all but the number of parameterized beams which is 2 at each time step. Source
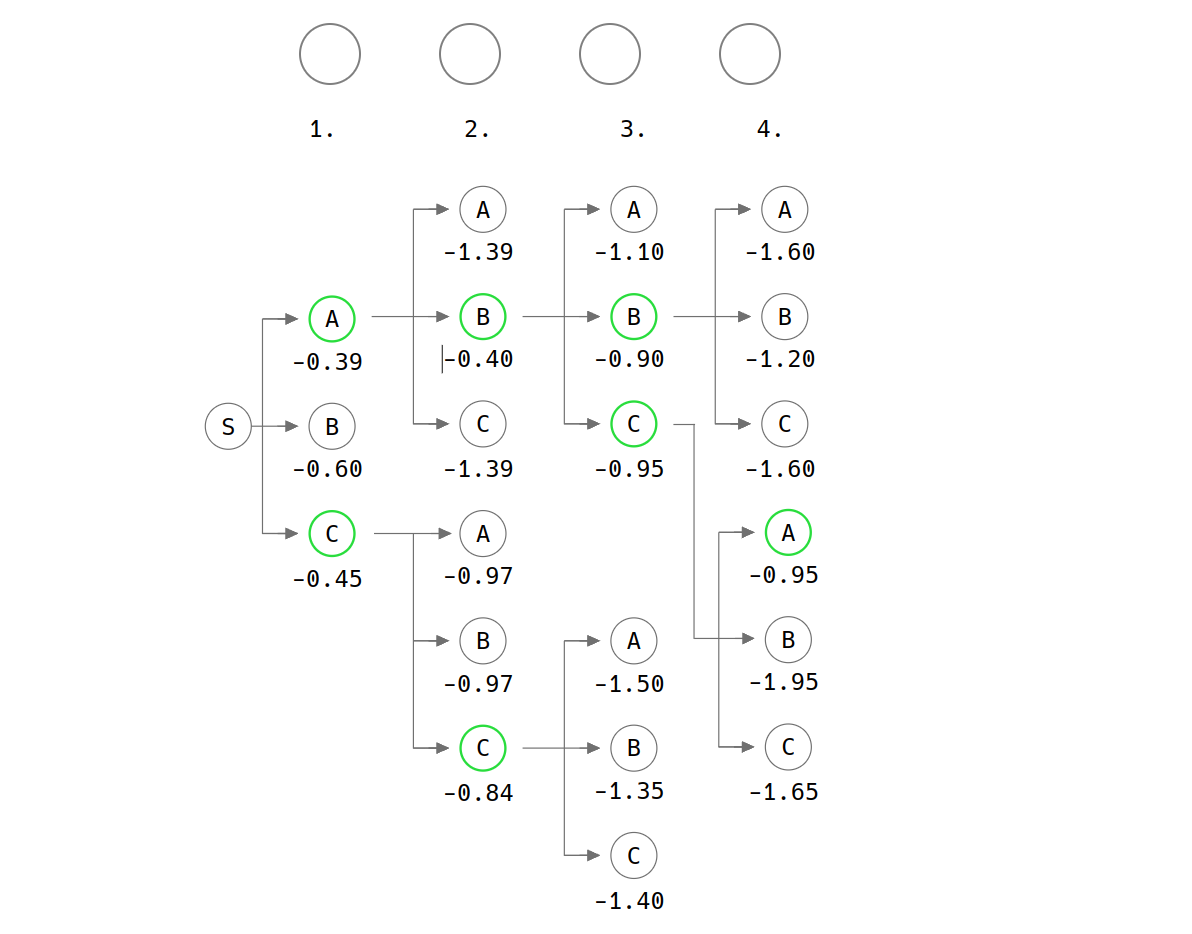
With the theoretical foundation in place, it is time to transition to the practical side of things. Let’s start by implementing beam search in PyTorch. This code is directly derived from this Repo.
class Beam:
def __init__(self, device, size, input_ids, score, output=None):
self.device = device
self.size = size # num_beam
self.input_ids = input_ids.to(self.device)
self.score = score
self.output = output.to(self.device) if output is not None else None
# get input_ids
def get_current_state(self):
return self.input_ids
# get probability of the sentence
def get_score(self):
return self.score
# create a new instance of Beam class after the top k selection
def extend(self, token_id, score):
new_input_ids = torch.cat([self.input_ids, token_id.unsqueeze(0)], dim=-1)
new_score = self.score * score
new_output = torch.cat([self.output, token_id.unsqueeze(0)], dim=-1) if self.output is not None else new_input_ids
return Beam(self.device, self.size, new_input_ids, new_score, new_output)
class BeamSampler(Sampler):
def beam_decode(self, ids):
return self.tokenizer.decode(ids.squeeze().tolist())
# Get the top k id with the greatest probability
@staticmethod
def get_topk(prob, k=1):
scores, token_ids = torch.topk(prob, k=k, dim=-1)
return scores, token_ids
def __call__(self, prompt, max_new_tokens=10, num_beam=1):
input_ids = self.encode(prompt)
# initialize the beam
# Ensure this initializes only `num_beam` beams
beams = [Beam(self.device, num_beam, input_ids, 1) for _ in range(num_beam)]
# loop until the maximum length is reached
for i in range(max_new_tokens):
all_next_token_prob = []
for beam in beams:
next_token_prob = self.get_next_token_prob(input_ids=beam.get_current_state())
all_next_token_prob.append(next_token_prob)
# With this
all_topk_scores = []
all_topk_token_ids = []
for prob in all_next_token_prob:
scores, token_ids = self.get_topk(prob, k=num_beam)
all_topk_scores.append(scores)
all_topk_token_ids.append(token_ids)
all_topk_scores = torch.stack(all_topk_scores)
all_topk_token_ids = torch.stack(all_topk_token_ids)
new_beams = []
# Then, when accessing them:
for j, beam in enumerate(beams):
for k in range(num_beam):
score = all_topk_scores[j][k].item()
token_id = all_topk_token_ids[j][k].unsqueeze(0)
new_beam = beam.extend(token_id, score)
new_beams.append(new_beam)
beams = sorted(new_beams, key=lambda b: b.get_score(), reverse=True)[:num_beam]
generated_text = self.beam_decode(beams[0].output[:, len(input_ids[0]):])
return prompt + generated_text
beam_sampler = BeamSampler()
result = beam_sampler(prompt=SAMPLE_TEXT,max_new_tokens=16 , num_beam=1)
print(result)
result = beam_sampler(prompt=SAMPLE_TEXT,max_new_tokens=16 , num_beam=10)
print(result)
Output:
Artificial Intelligence is the intelligence possessed by the machines that run the world. It is the intelligence that is capable of understanding and
Artificial Intelligence is the intelligence possessed by the machines used to create those machines.[1e]] As such we may expect intelligent
When we used a beam size of 1, the generated text was more deterministic, relying heavily on the most probable tokens at each step. On the other hand, increasing the beam size to 10 allowed for a broader exploration of possibilities, which resulted in coherent text with a degree of variation.
However, there are a few drawbacks to this approach:
- It requires more computational resources than greedy search, as it needs to maintain and calculate probabilities for ‘k’ sequences at each step which can amplify inference time.
- It also doesn’t guarantee finding the most probable sequence, especially if the beam width ‘k’ is too small compared to the size of the vocabulary.
Temperature Sampling
$$ P\left(x_{i} \mid x_{1: i-1}\right)=\frac{\exp \left(u_{i} / t\right)}{\sum_{j} \exp \left(u_{j} / t\right)} $$
Random sampling can be very unpredictable. We can enhance the predictability and control over random sampling using temperature. Temperature serves as a mechanism to control the likelihood of selecting certain tokens over others. The temperature acts as a hyperparameter that can either amplify or reduce the randomness in the sampling process, providing a balance between unpredictability and determinism.
A temperature value set between 0 and 1 can adjust this probability. Specifically, as the temperature approaches 1, it tends to retain the original randomness of sampling. Conversely, as the temperature nears 0, the process becomes more deterministic like greedy decoding. Let’s see how this works on code:
class RandomTempSampler(Sampler):
def __call__(self, prompt, max_new_tokens=10 , temp : float = 0.5):
predictions = []
result = prompt
# generate until max_len
for i in range(max_new_tokens):
input_ids = self.encode(result)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
# apply temp before softmax (sharper logits)
next_token_probs /= temp
# convert logits to scores
scores = softmax(next_token_probs, dim=-1)
# sample from scores
id = torch.multinomial(scores, num_samples=1).item()
# convert to token and add new token to text
result += self.decode(id)
# keep track of scores for next token
predictions.append(scores[id].item())
return result
def sample_plot(self,prompt,temp:float = 0.5):
input_ids = self.encode(prompt)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
next_token_probs /= temp
scores = softmax(next_token_probs, dim=0)
self.plot_scores(scores=scores,title=f"Tempreature : {temp}",samples=10)
random_tempreature = RandomTempSampler()
print(random_tempreature(prompt=SAMPLE_TEXT,max_new_tokens=16,temp=0.1))
print(random_tempreature(prompt=SAMPLE_TEXT,max_new_tokens=16,temp=0.9))
Output:
Artificial Intelligence is the intelligence possessed by the machines that run the world. It is the intelligence that is able to understand and
Artificial Intelligence is the intelligence possessed by the computer when the parts of it that commands it do the work are no longer useful
Let’s look at the probability distribution when we change the temperature of the softmax function.
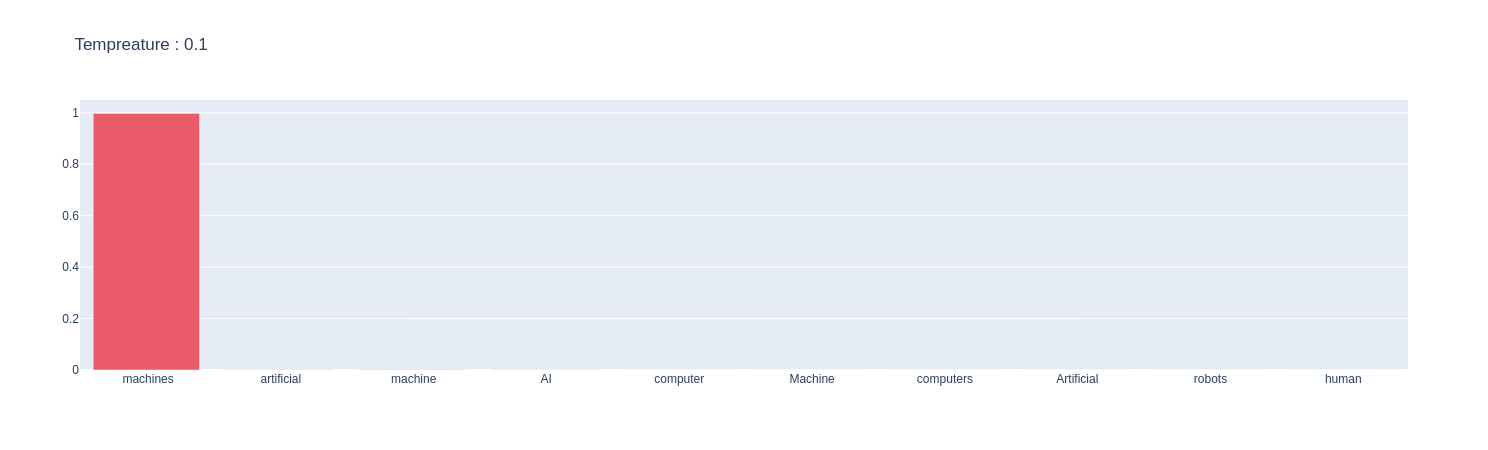
When Temperature is set to 0.1 :
random_tempreature.sample_plot(prompt=SAMPLE_TEXT,temp=0.1)
When Temperature is set to 0.9 :
random_tempreature.sample_plot(prompt=SAMPLE_TEXT,temp=0.1)
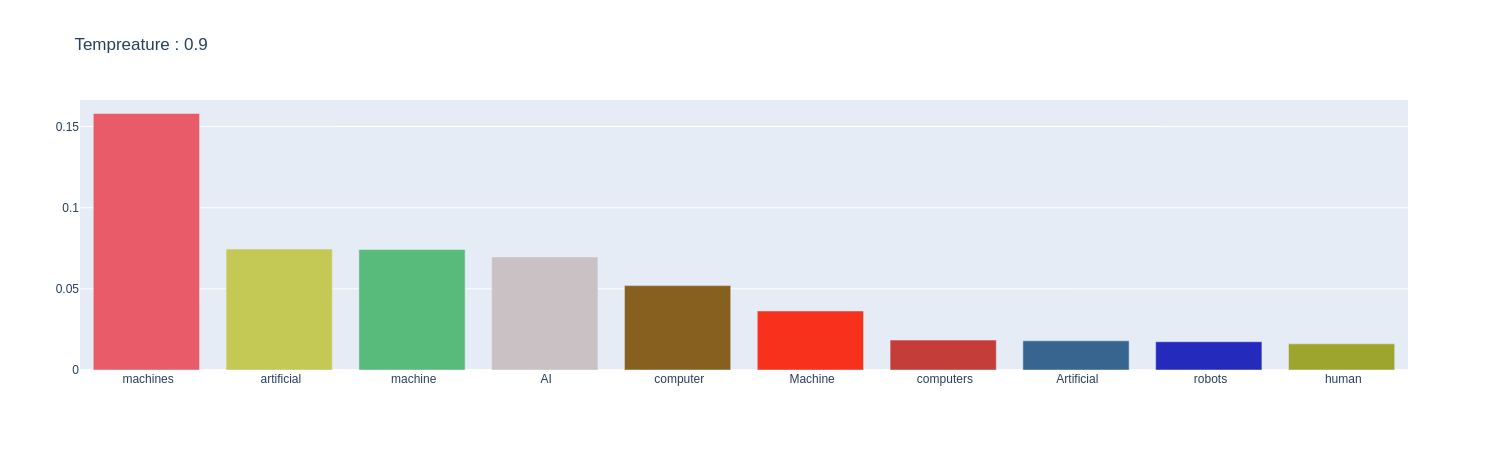
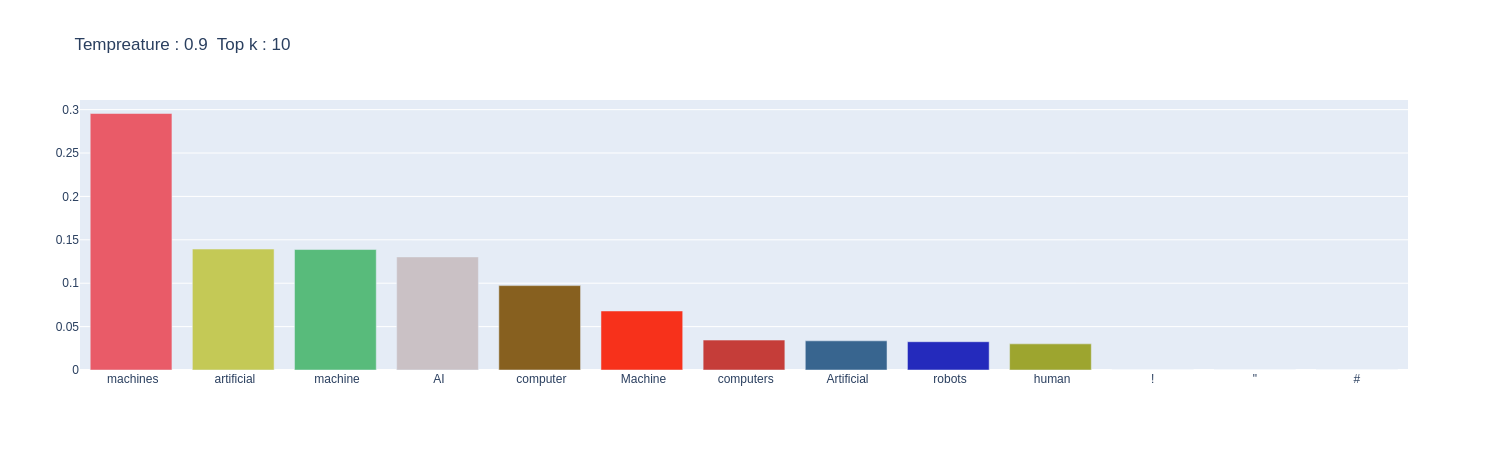
It is evident from the plots that by increasing the temperature, a skewed distribution is turned into a more uniform distribution. This will increase entropy and add more randomness. This is why, when we significantly raise the temperature, it introduces more randomness in the model, which can lead to unusual outputs.
Top-K sampling
Top-K sampling is another technique in language generation. It works by ensuring that only the most probable tokens (the top K tokens) have a chance at being selected in the next step.
This method narrows down the choices to the K most probable ones, and at each generation step, tokens are selected from this restricted pool. If we set $K=1$, it simply becomes a greedy search, choosing the most probable word each time. Conversely, if $k=len(vocabulary(v))$, it’s the same as pure sampling, considering every word equally. We can also introduce the concept of temperature in top-k sampling, which allows for the adjustment of randomness in top-k selections.
However, it’s crucial to note a limitation of this method. Using a constant value for k is not optimal for all contexts. In some situations, there can be many equally good options for the next word, making the distribution head flat. In other contexts, a few tokens dominate the probability distribution. A small k might result in generic text, and a large k could include unsuitable word candidates.
As we have now laid the theoretical groundwork, let’s implement top-k sampling with temperature.
class TOPKsampler(Sampler):
def __call__(self, prompt, max_new_tokens=10 ,top_k = 1 ,temp : float = 0.5):
predictions = []
result = prompt
# generate until max_len
for i in range(max_new_tokens):
# convert words to tokens
input_ids = self.encode(result)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
next_token_probs = next_token_probs / temp
indices_to_remove = next_token_probs < torch.topk(next_token_probs, top_k)[0][..., -1, None]
new_logits = torch.clone(next_token_probs)
new_logits[indices_to_remove] = float('-inf')
# convert logits to scores
scores = softmax(new_logits, dim=-1) # Use modified logits
# sample from scores
id = torch.multinomial(scores, num_samples=1).item()
# convert to token and add new token to text
result += self.decode(id)
# keep track of scores for next token
predictions.append(scores[id].item())
return result
def sample_plot(self,prompt ,top_k = 5 ,temp : float = 0.5):
input_ids = self.encode(prompt)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
next_token_probs = next_token_probs / temp
# Remove all tokens with a probability less than the last token of the top-k.
indices_to_remove = next_token_probs < torch.topk(next_token_probs, top_k)[0][..., -1, None]
new_logits = torch.clone(next_token_probs)
new_logits[indices_to_remove] = float('-inf')
# convert logits to scores
scores = softmax(new_logits, dim=-1) # Use modified logits
self.plot_scores(scores,title=f"Tempreature : {temp} Top k : {top_k}" , samples = top_k + int(math.sqrt(top_k)))
topksampler = TOPKsampler()
result = topksampler(
prompt=SAMPLE_TEXT,
max_new_tokens=32,
top_k= 10,
temp=0.5
)
print(result)
Output:
Artificial Intelligence is the intelligence possessed by the computers that control our lives. Artificial Intelligence is also the intelligence that runs our economy, our government, and our economy's own intelligence.
Let’s look at the probability distribution when we change the temperature of the softmax function among top-k tokens.
topksampler.sample_plot(prompt=SAMPLE_TEXT,top_k=10,temp=0.1)
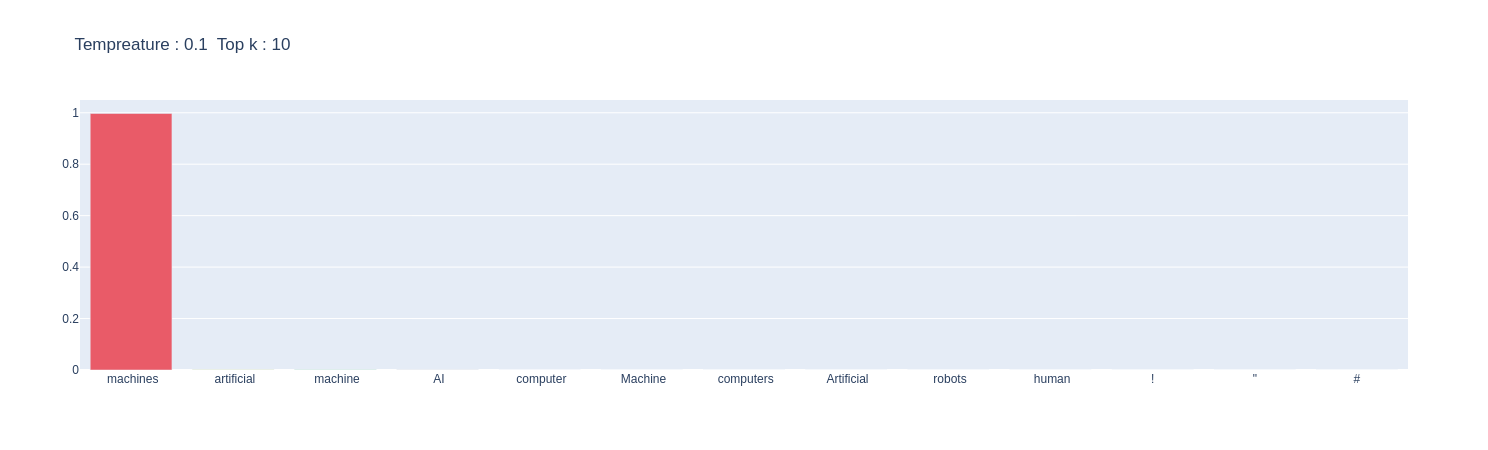
topksampler.sample_plot(prompt=SAMPLE_TEXT,top_k=10,temp=0.9)
Nucleus(top-p) sampling
Nucleus sampling is similar to Top-K sampling. Instead selecting the most probable K words, nucleus sampling selects the smallest set of words whose combined probabilities surpass a threshold, p. This method allows for a dynamic number of candidate words, which can expand or contract based on the model’s confidence in the vocabulary.
Nucleus sampling first picks a subset of the vocabulary $V^{(p)}$⊂$V$, where $V^{(p)}$ is smallest set of tokens such that
$$ \sum_{x_{i} \in V^{(p)}} P\left(x_{i} \mid x_{1: i-1}\right) \geq p $$
That is, we pick the highest probable tokens until the sum of their probabilities is less than p. Source
class NucleusSampler(Sampler):
def __call__(self, prompt, max_new_tokens=10 , p : float = 0.7):
predictions = []
result = prompt
# generate until max_len
for i in range(max_new_tokens):
# convert words to tokens
input_ids = self.encode(result)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
sorted_logits, sorted_indices = torch.sort(next_token_probs, descending=True)
cumulative_probs = torch.cumsum(softmax(sorted_logits, dim=-1), dim=-1)
# Remove tokens with cumulative probability above the threshold
sorted_indices_to_remove = cumulative_probs > p
"""
When we determine which tokens to remove based on this mask, it's important to note that as soon as the cumulative probability crosses the threshold `p`,
all the subsequent tokens will also have cumulative probabilities greater than `p` (because the probabilities are sorted in descending order).
The logic here is to also exclude the very first token that caused the cumulative sum to cross the threshold, and this is achieved by shifting the mask to the right.
By doing this shift and ensuring the first token that exceeds the threshold is included in the removal list,
we're adhering to the true spirit of top-p sampling: we're including in the final consideration only those tokens whose cumulative sum is less than or equal to `p`.
"""
# Shift the indices to the right to keep also the first token above the threshold
sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
sorted_indices_to_remove[..., 0] = 0
indices_to_remove = sorted_indices[sorted_indices_to_remove]
new_logits = torch.clone(next_token_probs)
new_logits[indices_to_remove] = float('-inf')
# convert logits to scores
scores = softmax(new_logits, dim=-1) # Use modified logits
# sample from scores
id = torch.multinomial(scores, num_samples=1).item()\
# convert to token and add new token to text
result += self.decode(id)
# keep track of scores for next token
predictions.append(scores[id].item())
return result
def sample_plot(self,prompt, p: float):
input_ids = self.encode(prompt)
next_token_probs = self.get_next_token_prob(input_ids=input_ids)
sorted_logits, sorted_indices = torch.sort(next_token_probs, descending=True)
cumulative_probs = torch.cumsum(softmax(sorted_logits, dim=-1), dim=-1)
# Remove tokens with cumulative probability above the threshold
sorted_indices_to_remove = cumulative_probs > p
# Shift the indices to the right to keep also the first token above the threshold
sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
sorted_indices_to_remove[..., 0] = 0
indices_to_remove = sorted_indices[sorted_indices_to_remove]
new_logits = torch.clone(next_token_probs)
new_logits[indices_to_remove] = float('-inf')
# convert logits to scores
scores = softmax(new_logits, dim=-1)
self.plot_scores(scores,title=f"P : {p}", samples=10)
nssammpler = NucleusSampler()
result = nssammpler(prompt=SAMPLE_TEXT,max_new_tokens=16,p=0.8)
print(result)
Output:
Artificial Intelligence is the intelligence possessed by the sentient, intellectual, or creative faculties, such as the abilities of people with hands
Let’s look at the number of candidate words distribution when we change the p value.
nssammpler.sample_plot(prompt=SAMPLE_TEXT,p=0.8)
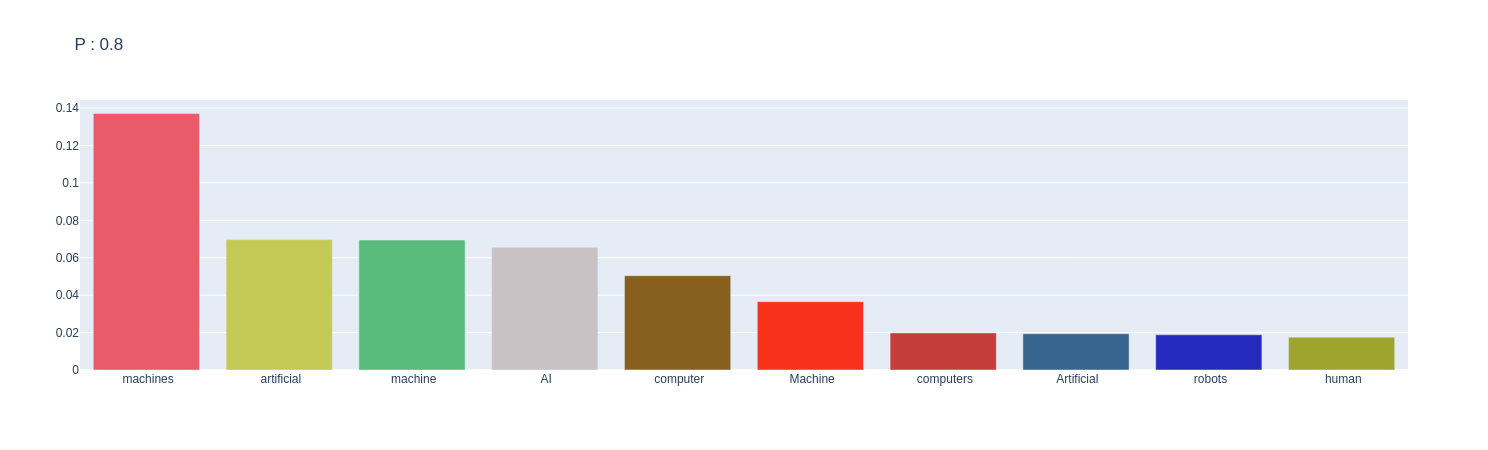
nssammpler.sample_plot(prompt*=SAMPLE_TEXT,p=0.1)
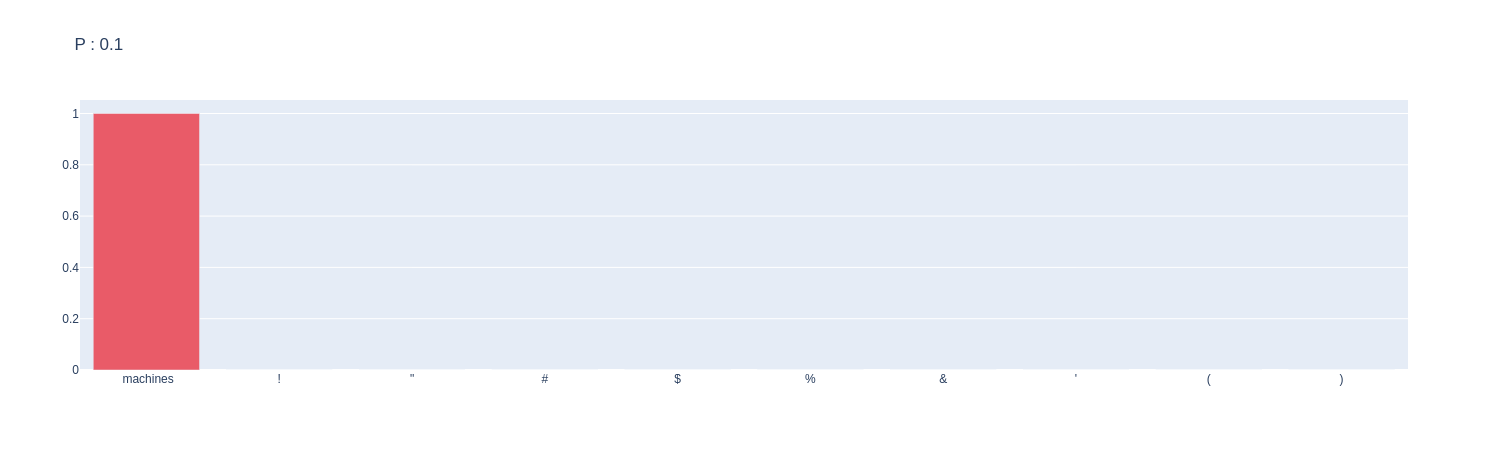
We can see from the plots that by increasing the p, the candidate words distribution converts from more uniform distribution to a skewed distribution.
All of the codes used in this repository can be found HERE. From the simplicity of Greedy Search Decoding to the more sophisticated approaches like Beam Search and various sampling techniques such as Temperature Sampling, Top-K, and Nucleus Sampling, each offers unique advantages to address specific challenges. By understanding and implementing these methods, we can tailor their model’s output to align closer with the desired outcome.
References
- https://www.kaggle.com/code/sajjadayobi360/how-to-generate-text-using-language-models
- https://github.com/rohan-paul/MachineLearning-DeepLearning-Code-for-my-YouTube-Channel/blob/master/NLP/Decoding_Strategies_for_text_generation/Decoding_Strategies_for_text_generation.ipynb
- https://vitalflux.com/greedy-search-vs-beam-search-decoding-concepts-examples/#:~:text=complex decoding methods.-,Drawbacks of Greedy Search Decoding Method,term implications of its choices.
- https://medium.com/@jessica_lopez/understanding-greedy-search-and-beam-search-98c1e3cd821d
- https://towardsdatascience.com/decoding-strategies-that-you-need-to-know-for-response-generation-ba95ee0faadc#:~:text=Random Sampling with Temperature,1%2C there is no effect.
- https://windysavage.github.io/Decoding-strategies-in-text-generation/
- https://peterchng.com/blog/2023/05/02/token-selection-strategies-top-k-top-p-and-temperature/