Introduction
In the rapidly evolving world of machine learning, one of the fundamental challenges is to make deep learning models run more efficiently. Model quantization is a strategy that allows for the reduction of memory requirements and computational needs, making the deployment of such models on hardware with constrained resources feasible and more efficient. In this blog, we’re going to take a deep dive into the realm of PyTorch model quantization.
We will first design and train a custom deep-learning architecture using PyTorch.Once our model is trained and ready, we’ll walk through the process of applying three distinct quantization techniques: static quantization, dynamic quantization, and quantization-aware training. Each of these techniques carries its unique strengths and potential limitations, contributing differently to the model’s performance and efficiency. Our objective will be to grasp not just the hows, but also the whys of PyTorch model quantization. We’ll see how each strategy affects the size, speed, and accuracy of the model. So, let’s get started!
Deep Dive into Quantization
Model quantization is the process of reducing the numerical precision of the weights and biases of a model. This process is crucial because it reduces the model size and speeds up inference, making real-time applications possible. The precision reduction is typically from floating-point numbers to integers that need less memory and computational power.
Quantization in deep neural networks is a crucial optimization technique, primarily needed for reducing model size, increasing computational efficiency, enhancing energy efficiency, and ensuring hardware compatibility. By truncating the numerical precision of parameters (weights and biases), quantization can substantially shrink the model’s memory footprint, making it easier to store and deploy. The practice also improves computational speed, making it essential for real-time applications. Moreover, it can reduce energy consumption, a critical concern for edge devices like mobile phones or IoT devices. Lastly, certain hardware accelerators are optimized for lower-precision computations, making quantization key to maximizing these optimizations. Although a trade-off exists as some accuracy may be lost due to reduced precision, various techniques are used to manage this.
Setting Up the Model
We’ll use a straightforward yet effective architecture to classify the MNIST dataset, a popular dataset containing grayscale images of handwritten digits. This simple deep learning model was chosen to highlight the power and effectiveness of model quantization without the complexity of a more elaborate architecture This architecture will consist Conv2d, BatchNorm2d, MaxPool2d, Linear, and ReLU blocks.
import warnings
warnings.filterwarnings("ignore")
import os
import torch
import torchvision
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.utils.data import DataLoader
import torchvision.transforms as transforms
Architecture :
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1)
self.bn1 = nn.BatchNorm2d(32)
self.relu1 = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1)
self.bn2 = nn.BatchNorm2d(64)
self.relu2 = nn.ReLU(inplace=True)
self.maxpool = nn.MaxPool2d(2, 2) # Initialized here
self.fc1 = nn.Linear(7*7*64, 512)
self.relu3 = nn.ReLU(inplace=True)
self.fc2 = nn.Linear(512, 10)
def forward(self, x):
x = self.conv1(x)
x = self.bn1(x)
x = self.relu1(x)
x = self.maxpool(x)
x = self.conv2(x)
x = self.bn2(x)
x = self.relu2(x)
x = self.maxpool(x)
x = x.reshape(x.shape[0], -1)
x = self.fc1(x)
x = self.relu3(x)
x = self.fc2(x)
return x
Dataset and Dataloaders:
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
trainset = torchvision.datasets.MNIST(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64,
shuffle=True, num_workers=16, pin_memory=True)
testset = torchvision.datasets.MNIST(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64,
shuffle=False, num_workers=16, pin_memory=True)
I will be using my ClassifierTrainer class to train the model. This class contains methods to train the model, save the model, and plot the accuracy and loss plot. All the helper methods and classes that we will be using here can be found in my GitHub repo.
from train_helpers import ClassifierTrainer,save_plots
unqant_model = Net() # The unquantized model.
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(unqant_model.parameters(), lr=0.01)
trainer = ClassifierTrainer(
model= unqant_model,
optimizer=optimizer,
criterion=criterion,
train_loader=trainloader,
val_loader=testloader,
num_epochs=4,
cuda=False
)
trainer.train()
save_plots(
train_acc=trainer.train_accs,
train_loss=trainer.train_losses,
valid_acc=trainer.val_accs,
valid_loss=trainer.val_losses,
)
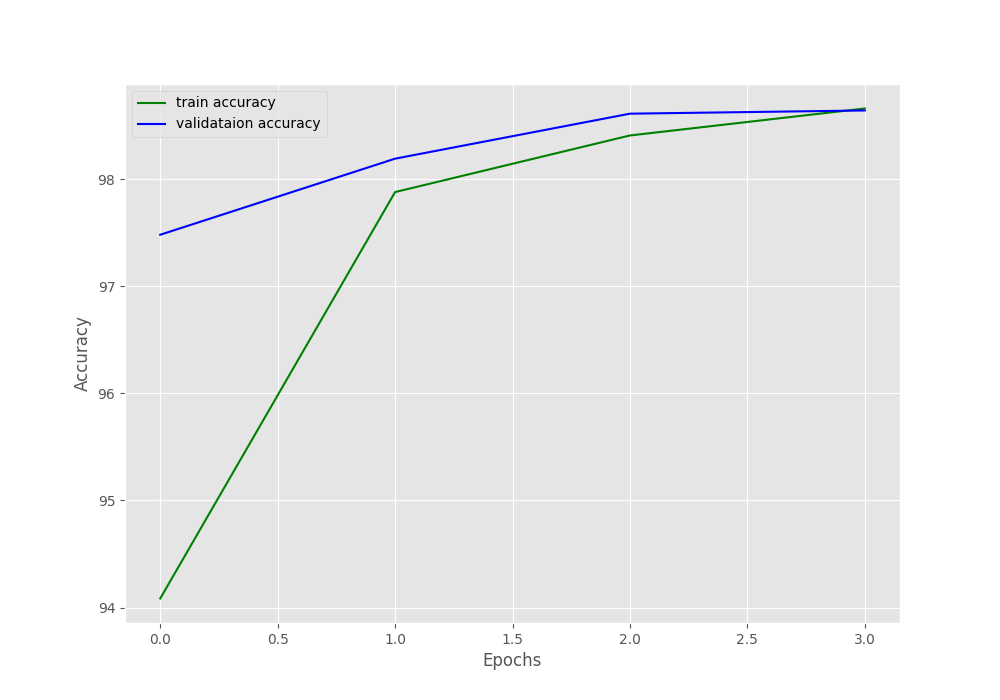
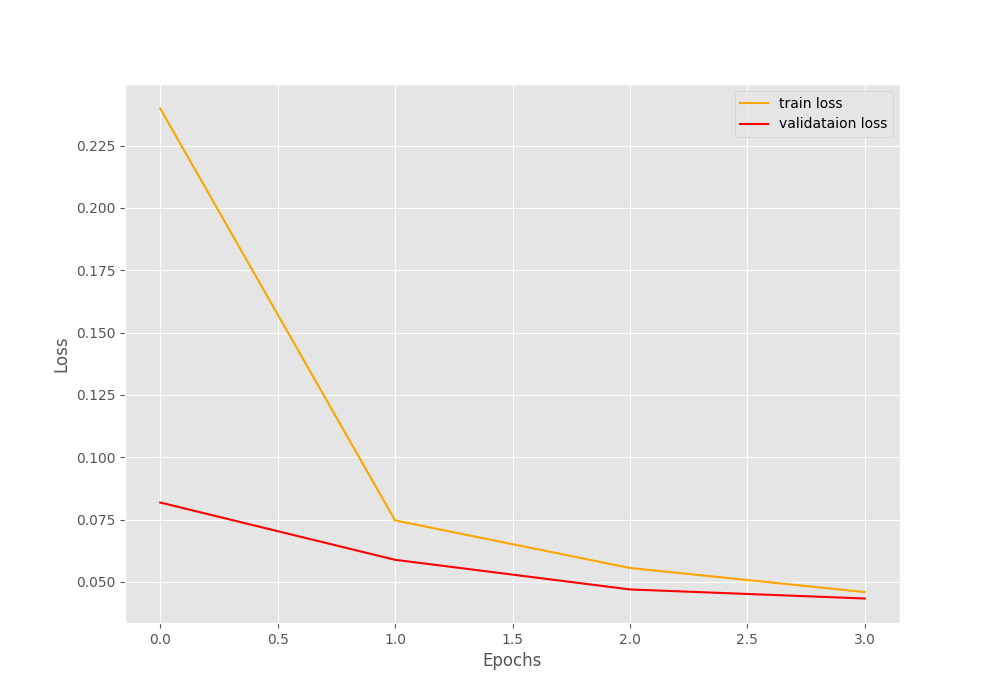
Epoch : 1/4: 100%|██████████| 938/938 [00:17<00:00, 55.13it/s, Accuracy=94.085, Loss=0.008]
Validation Accuracy: 97.48% and Loss: 0.08185123530910558
Best validation loss: 0.08185123530910558
Saving best model for epoch: 1
Epoch : 2/4: 100%|██████████| 938/938 [00:15<00:00, 59.86it/s, Accuracy=97.878, Loss=0.0259]
Validation Accuracy: 98.19% and Loss: 0.0588834396460402
Best validation loss: 0.0588834396460402
Saving best model for epoch: 2
Epoch : 3/4: 100%|██████████| 938/938 [00:15<00:00, 59.80it/s, Accuracy=98.407, Loss=0.0345]
Validation Accuracy: 98.61% and Loss: 0.04700030308571988
Best validation loss: 0.04700030308571988
Saving best model for epoch: 3
Epoch : 4/4: 100%|██████████| 938/938 [00:15<00:00, 59.63it/s, Accuracy=98.658, Loss=0.0237]
Validation Accuracy: 98.64% and Loss: 0.043366746839516274
Best validation loss: 0.043366746839516274
Saving best model for epoch: 4
Types of Model Quantization
Now, as our model is being trained, let’s dive deeper into quantization. PyTorch offers three distinct quantization methods, each differentiated by how the bins for converting fp32 to int8 are established. Each of these three PyTorch quantization strategies has unique ways of adjusting the quantization algorithm and deciding the bins used to transform the float 32 vectors into int8. As a result, each method brings its own set of benefits and potential limitations.
- Static Quantization
- Dynamic Quantization
- Quantization-Aware Training
Static Quantization / Post-Training Static Quantization
Static Quantization, also known as post-training quantization, is the most common form of quantization. It’s applied after the model training is complete. Here, both weights and activations of the model are quantised to lower precision. The scales and zero points for static quantization are calculated before inference using a representative dataset, in contrast to dynamic quantization, where they were gathered during inference.
Since the quantization process happens offline after training, there’s no runtime overhead for quantizing weights and activations. Quantized models are usually compatible with hardware accelerators designed for low-precision computation, enabling even faster inference.
However, Converting from high-precision weights and activations to lower precision can lead to a slight drop in model accuracy. Also, you need representative data for the calibration step in static quantization. It’s crucial to select a dataset that closely resembles the data the model will see in production.
Steps for Static Quantization:
Step 1. Set the model to evaluation mode with model.eval(). This is important as certain layers like dropout and batchnorm behave differently during training and evaluation.
import copy
unqant_model_copy = copy.deepcopy(unqant_model)
unqant_model_copy.eval()
Net(
(conv1): Conv2d(1, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(bn1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu1): ReLU(inplace=True)
(conv2): Conv2d(32, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu2): ReLU(inplace=True)
(maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(fc1): Linear(in_features=3136, out_features=512, bias=True)
(relu3): ReLU(inplace=True)
(fc2): Linear(in_features=512, out_features=10, bias=True)
)
Step 2. Define the list of layers in your model architecture that can be fused together for the purpose of quantization. When performing quantization, certain groups of operations can be replaced by single operations that are equivalent but more computationally efficient. For example, a convolution followed by a batch normalization, followed by a ReLU operation (Conv -> BatchNorm -> ReLU), can be replaced by a single fused ConvBnReLU operation. We will use torch.quantization.fuse_modules to fuse a list of modules into a single module. This has several advantages:
-
Performance Improvement: By fusing multiple operations into one, the fused operation can be faster than the individual operations due to fewer function calls and less data movement.
-
Memory Efficiency: Fused operations reduce the need for intermediate results. This can significantly reduce memory usage, especially for large models and inputs.
-
Simplified Model Graph: The process of fusing operations can simplify the model graph, making it easier to understand and optimize.
Our model architecture contains 2 (Conv -> BatchNorm -> ReLU) blocks. We can combine these blocks into a ConvBnReLU block.
fused_layers = [['conv1', 'bn1', 'relu1'], ['conv2', 'bn2', 'relu2']]
fused_model = torch.quantization.fuse_modules(unqant_model_copy, fused_layers, inplace=True)
Step 3. Next, we will use the QuantizedModel wrapper class to wrap our model.
class QuantizedModel(torch.nn.Module):
def __init__(self, model):
super().__init__()
self.model_fp32 = model
self.quant = torch.quantization.QuantStub()
self.dequant = torch.quantization.DeQuantStub()
def forward(self, x):
x = self.quant(x)
x = self.model_fp32(x)
x = self.dequant(x)
return x
The essence of this code is to add quantization and dequantization stubs to the model, which will act as ‘anchors’ to insert the actual quantization and dequantization functions in the model graph during the quantization process. The quant_layer converts the numbers in fp32 to int8 so that conv and relu will run in int8 format and then the dequant_layer will perform the int8 to fp32 conversion.
Step 4. Set the configuration for quantization using the get_default_qconfig function from torch.quantization. T
# Select quantization schemes from
# https://pytorch.org/docs/stable/quantization-support.html
quantization_config = torch.quantization.get_default_qconfig("fbgemm")
quantized_model.qconfig = quantization_config
# Print quantization configurations
print(quantized_model.qconfig)
“fbgemm” is a high-performance, 8-bit quantization backend that is used on CPUs. It’s currently the recommended backend for quantization when deploying on servers. The qconfig attribute of a PyTorch model is used to specify how the model should be quantized. By assigning quantization_config to quantized_model.qconfig, you’re specifying that the model should be quantized according to the “fbgemm” backend’s default configuration.
Step 5. Prepare the model for quantization with the torch.quantization.prepare() function. The model is prepared in-place.
torch.quantization.prepare(quantized_model, inplace=True)
Step 6. Calibrate the model with the test dataset. Run the model with a few examples to calibrate the quantization process.
def calibrate_model(model, loader, device=torch.device("cpu")):
model.to(device)
model.eval()
for inputs, labels in loader:
inputs = inputs.to(device)
labels = labels.to(device)
_ = model(inputs)
# Use training data for calibration.
calibrate_model(model=quantized_model, loader=trainloader, device="cpu")
During the quantization process, floating-point values are mapped to integer values. For weights, the range is known as they’re static and don’t change post-training. However, activations can vary depending on the input to the network. Calibration, typically performed by passing a subset of the data through the model and collecting the outputs, helps estimate this range.
Step 7. Convert the prepared model to a quantized model using torch.quantization.convert(). The conversion is also done in-place.
quantized_model = torch.quantization.convert(quantized_model, inplace=True)
quantized_model.eval()
Model Comparison
The Static quantization process is now completed. We can finally compare our quantized model to the unquantized model.
I have written a simple helper class to compare two models. The ModelCompare class will take two model and compare their size, accuracy, and average inference time over N iterations.
from utils import ModelCompare
model_compare = ModelCompare(
model1=quantized_model,
model1_info="Quantized Model",
model2=unqant_model,
model2_info="Uquantize model",
cuda=False
)
print("="*50)
model_compare.compare_size()
print("="*50)
model_compare.compare_accuracy(dataloder=testloader)
print("="*50)
model_compare.compare_inference_time(N=2 , dataloder=testloader)
Result:
Model Quantized Model Size(Mb): 1.648963
Model Uquantize model Size(Mb): 6.526259
______________________________________________
The Quantized Model is smaller by 74.73%.
Accuracy of Quantized Model: 98.5
Accuracy of Uquantize model: 98.53
Average inference time of Quantize model over 2 iterations: 0.6589450836181641
Average inference time of Uquantize Model over 2 iterations: 0.7821568250656128
________________________________________________________________________________
The Quantize model is faster by 15.75%.
Dynamic Quantization
Dynamic quantization quantizes the model weights and is carried out dynamically during runtime. The activations are stored in their original floating-point format.
Since weights are quantized dynamically at runtime, it allows for more flexibility. It can be beneficial in handling cases where the range of values can vary. As activations remain in their original format, the accuracy loss is usually less than static quantization. Dynamic quantization doesn’t need calibration data, making it simpler to apply.
However, as dynamic quantization only quantizes the weights, not the activations, it provides less compression and speedup than static quantization. Since weights are quantized on-the-fly during inference, it may introduce some runtime overhead.
Dynamic Quantization is pretty straightforward and requires only a single step for quantization. Let’s load our Unquantized model’s weight:
# load the torch state
state = torch.load("outputs/best_model.pth")
model = Net()
# loading the state dict
model.load_state_dict(state['model_state_dict'])
Set the model to eval() mode.
model.eval()
Perform dynamic quantization:
from utils import ModelCompare
model_compare = ModelCompare(
model1=quantized_model,
model1_info="Quantized Model",
model2=model,
model2_info="Unquantized Model",
cuda=False
)
Compare the quantized model with unquantized:
print("="*50)
model_compare.compare_size()
print("="*50)
model_compare.compare_accuracy(dataloder=testloader)
print("="*50)
model_compare.compare_inference_time(N=2 , dataloder=testloader)
Output :
==================================================
Model Quantized Model Size(Mb): 1.695323
Model Unquantized Model Size(Mb): 6.526259
The Quantized Model is smaller by 74.02%.
==================================================
Accuracy of Quantized Model: 98.54
Accuracy of Unquantized Model: 98.53
==================================================
Average inference time of Quantized Model over 2 iterations: 0.9944213628768921
Average inference time of Unquantized Model over 2 iterations: 0.9719561338424683
The Unquantized Model is faster by 2.26%.
Quantization Aware Training
Static quantization enables the generation of highly efficient quantized integer models for inference. However, despite careful post-training calibration, there may be instances where the model’s accuracy is compromised to an unacceptable extent. In such cases, post-training calibration alone is insufficient for generating a quantized integer model. To account for the quantization effect, the model needs to be trained in a manner that considers quantization. Quantization-aware training addresses this by incorporating fake quantization modules, which simulate the clamping and rounding effects of integer quantization at the specific points where quantization occurs during the conversion from floating-point to quantized integer models. These fake quantization modules also monitor the scales and zero points of the weights and activations. Once the quantization awareness training is completed, the floating-point model can be readily converted to a quantized integer model using the information stored in the fake quantization modules.
The Quantization Aware training process borrows similar steps from static quantizaion. Let’s load our Unquantized model’s weight:
# load the torch state
state = torch.load("outputs/best_model.pth")
quant_network = Net()
# loading the state dict
quant_network.load_state_dict(state['model_state_dict'])
Set the model to eval() mode.
quant_network.eval()
Step 1. Check the layers that can be fused and fuse the layers.
# check the layers that can be fused.
fused_layers = [['conv1', 'bn1', 'relu1'], ['conv2', 'bn2', 'relu2']]
# Fuse the layers
torch.quantization.fuse_modules(quant_network, fused_layers, inplace=True)
Step 2. Wrap the fused model using QuantizedModel.
class QuantizedModel(torch.nn.Module):
def __init__(self, model):
super().__init__()
self.model_fp32 = model
self.quant = torch.quantization.QuantStub()
self.dequant = torch.quantization.DeQuantStub()
def forward(self, x):
x = self.quant(x)
x = self.model_fp32(x)
x = self.dequant(x)
return x
# Apply torch.quantization.QuantStub() and torch.quantization.QuantStub() to the inputs and outputs, respectively.
quant_network = QuantizedModel(quant_network)
Step 3. Set the configuration for quantization
# Select quantization schemes from
quantization_config = torch.quantization.get_default_qconfig("fbgemm")
quant_network.qconfig = quantization_config
# Print quantization configurations
print(quant_network.qconfig)
Step 4. Prepare model for QAT.
# prepare for QAT
torch.quantization.prepare_qat(quant_network, inplace=True)
Step 5. Now, use our ClassifierTrainer to train the QAT model.
from train_helpers import ClassifierTrainer
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(quant_network.parameters(), lr=0.01)
trainer = ClassifierTrainer(
model= quant_network,
optimizer=optimizer,
criterion=criterion,
train_loader=trainloader,
val_loader=testloader,
cuda=False,
num_epochs=4
)
trainer.train(save_model=False)
Epoch : 1/4: 100%|██████████| 938/938 [00:18<00:00, 51.95it/s, Accuracy=77.492, Loss=0.2025]
Validation Accuracy: 92.54% and Loss: 0.2595426786074023
Epoch : 2/4: 100%|██████████| 938/938 [00:16<00:00, 55.84it/s, Accuracy=93.878, Loss=0.1657]
Validation Accuracy: 95.98% and Loss: 0.14535175562557426
Epoch : 3/4: 100%|██████████| 938/938 [00:16<00:00, 55.95it/s, Accuracy=96.143, Loss=0.0881]
Validation Accuracy: 96.3% and Loss: 0.11678009550680353
Epoch : 4/4: 100%|██████████| 938/938 [00:16<00:00, 55.86it/s, Accuracy=97.043, Loss=0.0618]
Validation Accuracy: 97.5% and Loss: 0.08276212103383106
Step 6. Finally, perform quantization on the model.
quant_network.to("cpu")
quantized_model = torch.quantization.convert(quant_network, inplace=True)
Model comparison
from utils import ModelCompare
model_compare = ModelCompare(
model1=quantized_model,
model1_info="Quantized Model",
model2=model,
model2_info="UnQuantized Model",
cuda=False
)
print("="*50)
model_compare.compare_size()
print("="*50)
model_compare.compare_accuracy(dataloder=testloader)
print("="*50)
model_compare.compare_inference_time(N=10 , dataloder=testloader)
==================================================
Model Quantized Model Size(Mb): 1.648963
Model UnQuantized Model Size(Mb): 6.526259
The Quantized Model is smaller by 74.73%.
==================================================
Accuracy of Quantized Model: 97.51
Accuracy of UnQuantized Model: 98.53
==================================================
Average inference time of Quantized Model over 10 iterations: 0.6605435371398926
Average inference time of UnQuantized Model over 10 iterations: 0.6626742124557495
The Quantized Model is faster by 0.32%.
Conclusion:
The broader implication of model quantization extends beyond just model efficiency and performance. By reducing computational needs, energy consumption, and memory requirements, we make advanced deep-learning models more accessible, especially on hardware with limited resources. This in turn paves the way for a broader and more diverse range of applications. In closing, I hope that this blog has equipped you with a better understanding of PyTorch model quantization, and inspires you to leverage these techniques in your deep learning journey. Happy coding!
References:
- https://towardsdatascience.com/inside-quantization-aware-training-4f91c8837ead
- https://www.youtube.com/watch?v=hGkTFa7FSE0
- https://deci.ai/quantization-and-quantization-aware-training/
- https://leimao.github.io/blog/PyTorch-Quantization-Aware-Training/
- https://intellabs.github.io/distiller/algo_quantization.html